Depth of Field Formulas

The basis of these formulas is given in the section Derivation of the DOF formulas refer to the diagram in that section for illustration of the quantities discussed below.

Hyperfocal Distance
Let f be the lens focal length, N be the lens f-number, and c be the circle of confusion for a given image format. The hyperfocal distance H is given by

Moderate-to-large distances
Let s be the distance at which the camera is focused (the “subject distance”). When s is large in comparison with the lens focal length, the distance D_N from the camera to the near limit of DOF and the distance D_F from the camera to the far limit of DOF are

When the subject distance is the hyperfocal distance,

The depth of field D_F − D_N is

For , the far limit of DOF is at infinity and the DOF is infinite; of course, only objects at or beyond the near limit of DOF will be recorded with acceptable sharpness.

Substituting for H and rearranging, DOF can be expressed as

Thus, for a given image format, depth of field is determined by three factors: the focal length of the lens, the f-number of the lens opening (the aperture), and the camera-to-subject distance.

Close-up
When the subject distance s approaches the focal length, using the formulas given above can result in significant errors. For close-up work, the hyperfocal distance has little applicability, and it usually is more convenient to express DOF in terms of image magnification. Let m be the magnification; when the subject distance is small in comparison with the hyperfocal distance,

so that for a given magnification, DOF is independent of focal length. Stated otherwise, for the same subject magnification, all focal lengths give approximately the same DOF. This statement is true only when the subject distance is small in comparison with the hyperfocal distance, however.

The discussion thus far has assumed a symmetrical lens for which the entrance and exit coincide with the front and rear pupils nodal planes, and for which the pupil magnification (the ratio of exit pupil diameter to that of the entrance pupil is unity. Although this assumption usually is reasonable for large-format lenses, it often is invalid for medium- and small-format lenses.

When , the DOF for an asymmetrical lens is

where P is the pupil magnification. When the pupil magnification is unity, this equation reduces to that for a symmetrical lens.

Except for close-up and macro photography, the effect of lens asymmetry is minimal. At unity magnification, however, the errors from neglecting the pupil magnification can be significant. Consider a telephoto lens with P = 0.5 and a retrofocus wide-angle lens with P = 2, at m = 1.0. The asymmetrical-lens formula gives DOF = 6Nc and DOF = 3Nc, respectively. The symmetrical-lens formula gives DOF = 4Nc in either case. The errors are −33% and 33%, respectively.

Focus and f-number from DOF limits
Not all images require that sharpness extend to infinity; for given near and far DOF limits D_N and D_F, the required f-number is smallest when focus is set to

When the subject distance is large in comparison with the lens focal length, the required f-number is

In practice, these settings usually are determined on the image side of the lens, using measurements on the bed or rail with a view camera, or using lens DOF scales on manual-focus lenses for small- and medium-format cameras. If v_N and v_F are the image distances that correspond to the near and far limits of DOF, the required f-number is minimized when the image distance v is

In practical terms, focus is set to halfway between the near and far image distances. The required f-number is

The image distances are measured from the camera's image plane to the lens's image nodal plane, which is not always easy to locate. In most cases, focus and f-number can be determined with sufficient accuracy using the approximate formulas above, which require only the difference between the near and far image distances; view camera users often refer to the difference 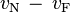as the focus spread. Most lens DOF scales are based on the same concept.

Foreground and background blur
If a subject is at distance s and the foreground or background is at distance D, let the distance between the subject and the foreground or background be indicated by

The blur disk diameter b of a detail at distance x_d from the subject can be expressed as a function of the focal length f, subject magnification m_s, and f-number N according to

The minus sign applies to a foreground object, and the plus sign applies to a background object.

The blur increases with the distance from the subject; when , the detail is within the depth of field, and the blur is imperceptible. If the detail is only slightly outside the DOF, the blur may be only barely perceptible.

For a given subject magnification, f-number, and distance from the subject of the foreground or background detail, the degree of detail blur varies with the lens focal length. For a background detail, the blur increases with focal length; for a foreground detail, the blur decreases with focal length. For a given scene, the positions of the subject, foreground, and background usually are fixed, and the distance between subject and the foreground or background remains constant regardless of the camera position; however, to maintain constant magnification, the subject distance must vary if the focal length is changed. For small distance between the foreground or background detail, the effect of focal length is small; for large distance, the effect can be significant. For a reasonably distant background detail, the blur disk diameter is

depending only on focal length.

The blur diameter of foreground details is very large if the details are close to the lens.

The ratio b / c is independent of camera format; the blur then is in terms of circles of confusion.

The magnification of the detail also varies with focal length; for a given detail, the ratio of the blur disk diameter to imaged size of the detail is independent of focal length, depending only on the detail size and its distance from the subject. This ratio can be useful when it is important that the background be recognizable (as usually is the case in evidence or surveillance photography), or unrecognizable (as might be the case for a pictorial photographer using selective focus to isolate the subject from a distracting background). As a general rule, an object is recognizable if the blur disk diameter is one-tenth to one-fifth the size of the object or smaller and unrecognizable when the blur disk diameter is the object size or greater.

The effect of focal length on background blur is illustrated in van Walree's article on Depth of Field.

Practical complications
The distance scales on most medium- and small-format lenses indicate distance from the camera's image plane. Most DOF formulas, including those in this article, use the object distance s from the lens's object nodal plane, which often is not easy to locate. Moreover, for many zoom lenses and internal-focusing non-zoom lenses, the location of the object nodal plane, as well as focal length, changes with subject distance. When the subject distance is large in comparison with the lens focal length, the exact location of the object nodal plane is not critical; the distance is essentially the same whether measured from the front of the lens, the image plane, or the actual nodal plane. The same is not true for close-up photography; at unity magnification, a slight error in the location of the object nodal plane can result in a DOF error greater than the errors from any approximations in the DOF equations.

The asymmetrical lens formulas require knowledge of the pupil magnification, which usually is not specified for medium- and small-format lenses. The pupil magnification can be estimated by looking into the front and rear of the lens and measuring the diameters of the apparent apertures, and computing the ratio (rear diameter divided by front diameter). However, for many zoom lenses and internal-focusing non-zoom lenses, the pupil magnification changes with subject distance, and several measurements may be required.

Limitations
Most DOF formulas, including those discussed in this article, employ several simplifications:

1. Paraxial (Gaussian) optics is assumed, and technically, the formulas are valid only for rays that are infinitesimally close to the lens axis. However, Gaussian optics usually is more than adequate for determining DOF, and non-paraxial formulas are sufficiently complex that requiring their use would make determination of DOF impractical in most cases.
   
   
2. Lens aberrations are ignored. Including the effects of aberrations is nearly impossible, because doing so requires knowledge of the specific lens design. Moreover, in well-designed lenses, most aberrations are well corrected, and at least near the optical axis, often are almost negligible when the lens is stopped down 2–3 steps from maximum aperture. Because lenses usually are stopped down at least to this point when DOF is of interest, ignoring aberrations usually is reasonable. Not all aberrations are reduced by stopping down, however, so actual sharpness may be slightly less than predicted by DOF formulas.
   
   
3. Diffraction is ignored. DOF formulas imply that any arbitrary DOF can be achieved by using a sufficiently large f-number . Because of diffraction, however, this isn't quite true. Once a lens is stopped down to where most aberrations are well corrected, stopping down further will decrease sharpness in the center of the field. At the DOF limits, however, further stopping down decreases the size of the defocus blur spot, and the overall sharpness may increase. Consequently, choosing an f-number sometimes involves a tradeoff between center and edge sharpness, although viewers typically prefer uniform sharpness to slightly greater center sharpness. The choice, of course, is subjective, and may depend upon the particular image. Eventually, the defocus blur spot becomes negligibly small, and further stopping down serves only to decrease sharpness even at DOF limits. Typically, diffraction at DOF limits becomes significant only at fairly large f-numbers; because large f-numbers typically require long exposure times, motion blur often causes greater loss of sharpness than does diffraction.
   
   
4. Post-capture manipulation of the image is ignored. Sharpening via techniques such as deconvolution or unsharp mask can increase the DOF in the final image, particularly when the original image has a large DOF. Conversely, image noise reduction can reduce the DOF.
   
   
5. For digital capture with color filter array sensors, demosaicing is ignored. Demosaicing alone would normally reduce the DOF, but the demosaicing algorithm used might also include sharpening.

The lens designer cannot restrict analysis to Gaussian optics and cannot ignore lens aberrations. However, the requirements of practical photography are less demanding than those of lens design, and despite the simplifications employed in development of most DOF formulas, these formulas have proven useful in determining camera settings that result in acceptably sharp pictures. It should be recognized that DOF limits are not hard boundaries between sharp and unsharp, and that there is little point in determining DOF limits to a precision of many significant figures.